Todos os creditos para Helmut Linde, que escreveu o excelente artigo (arXiv:1907.11311) do qual baseei todo esse texto.
Osciladores harmônicos quânticos
Comecemos com um problema da mecânica clássica: o Oscilador Harmônico Quântico (OHQ). Aqui, temos um oscilador harmônico simples (a famosa mola com F = -kx), só que quantizado. O parâmetro desta teoria será o $\hat{x}$ representando o deslocamento do oscilador. Livros normalmente usam $\hat{q}$, mas quero que esse texto seja condizente com o post anterior. O hamiltoniano é dado por:
$$ \hat{H} = \frac{\hat{p}^2}{2m} + \frac{1}{2}\kappa \hat{x}^2$$
O primeiro termo é a energia cinética usual e o segundo a energia potencial elástica, que também pode ser escrito como $\frac{1}{2}m\omega^2 \hat{x}^2$, pois $\omega = \sqrt{\kappa/m}$. Se você estudou mecânica quântica, e eu estou presumindo que sim, sabe que os auto-estados $\psi_n$ da equação $\hat{H}|\psi\rangle = E|\psi\rangle$ é dado por uma fórmula maluca e complexa que raramente é derivada nos livros:
$$ \psi_n = \frac{1}{\sqrt{2^n n!}} (\frac{m\omega}{\pi\hbar})^{1/4} e^{-\frac{m\omega x^2}{2\hbar}} H_n(\sqrt{\frac{m\omega}{\hbar}}x) $$
onde $H_n$ são os polinômios de Hermite. Também não me darei ao trabalho de derivar ela, mas ela é importante na hora de computar numericamente os valores do estado. Este trabalho porém residirá apenas à mim.
Válido lembrar também que utilizando os operadores de criação e aniquilação que são definidos por:
$$ a = \sqrt{\frac{m\omega}{2\hbar}}(\hat{x} + \frac{i}{m\omega}\hat{p}) $$ $$ a^\dagger = \sqrt{\frac{m\omega}{2\hbar}}(\hat{x} - \frac{i}{m\omega}\hat{p}) $$
E portanto permitem escrever o hamiltoniano de forma muito mais elegante:
$$ \hat{H} = \hbar\omega(a^\dagger a + \frac{1}{2})$$
E que se $\hat{H}\psi = E\psi$, então $\hat{H}(a^\dagger\psi) = (E + \hbar\omega)\psi$, ou seja, $a^\dagger$ cria um “pacote de energia” de $\hbar\omega$. Similarmente, $a$ remove o “pacote de energia” do estado. Outra forma de dizer isso de forma mais inequívoca é que $\psi_n = c_n (a^\dagger)^n\psi_0$ (onde $c_n$ é apenas uma constante de normalização).
Fazendo um gráfico do de $\psi_1$, por exemplo, temos:
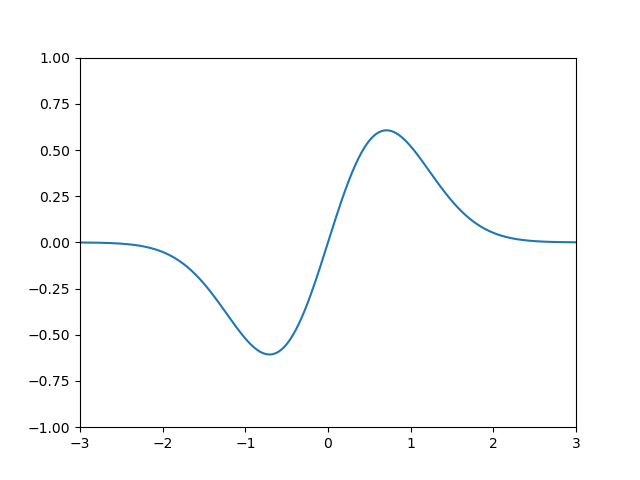
Porém, podemos representar tudo em uma única linha, usando cores ao invés de altura para representar o valor de $\psi_1$. Também rotacionei por 90 graus, pois será útil no futuro. Note também que eu não coloquei a cor para todos os pontos da linha, mas para um monte de pontos aleatórios uniformemente distribuídos na linha. Isso será útil no futuro também.
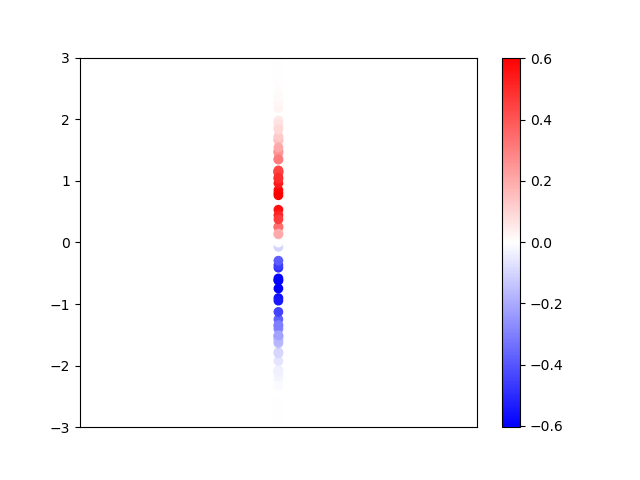
DOIS Osciladores harmônicos quânticos
Agora vamos supor dois osciladores harmônicos. Nosso estado dependerá de dois parâmetros agora, um para cada oscilador: $\hat{x}_1, \hat{x}_2$. Por hora, assumiremos que esses osciladores não interagem entre si. O hamiltoniano é:
$$ \hat{H} = \sum_{n=1,2} \frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega^2 \hat{x}_n^2 $$
Claro que esse hamiltoniano será generalizado para $N$ osciladores no futuro, mas ainda quero apenas olhar no caso $N=2$ para compreender os gráficos. Um fato interessante é que por não interagirem entre si, o auto-estado do hamiltoniano acima $\psi(\hat{x} _ 1, \hat{x} _ 2)$ onde um dos estados de energia é $\psi_{\nu_1}(\hat{x} _ 1)$ e outro $\psi_{\nu_2}(\hat{x} _ 2)$ é:
$$ \psi_{\nu_1, \nu_2}(\hat{x} _ 1, \hat{x} _ 2) = \psi_{\nu_1}(\hat{x} _ 1)\psi_{\nu_2}(\hat{x} _ 2) $$
Usando o mesmo método de pontos, como agora temos dois parâmetros vou colocar cada ponto não numa reta como antes, mas num retângulo, e a cor do ponto ainda representa a intensidade de $\psi$. Por exemplo, no caso $\psi_{1, 2}$, o gráfico fica:
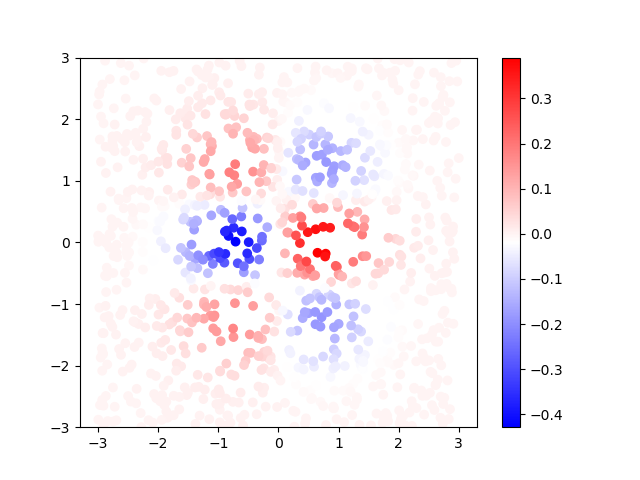
Outra possível representação, é ao invés de representar os parâmetros $\vec{x} = (\hat{x} _ 1, \hat{x} _ 2)$ como um ponto num espaço, podemos ter um eixo paralelo para cada parâmetro, e uma linha que conecte os dois pontos em cada eixo. Por exemplo, o ponto $\vec{x} = (0.759, 0.155)$ com $\psi_{1,2}(\vec{x}) = 0.396$ seria desenhado assim:
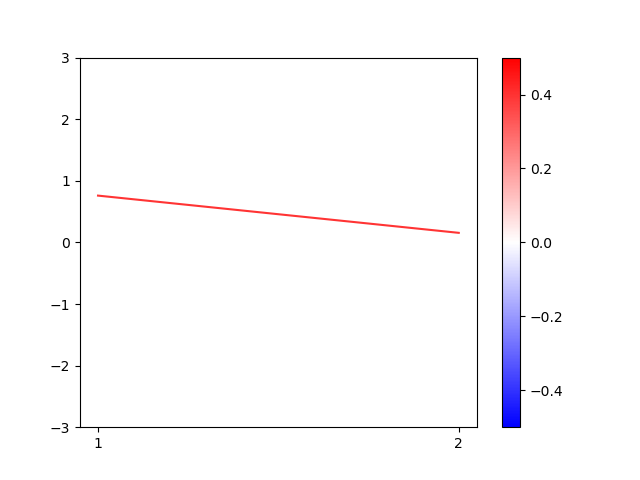
Logo, podemos fazer o mesmo gráfico de $\psi_{1,2}$, e agora entendemos porque eu usei pontos aleatório ao invés de todos os pontos. Não queremos infinitas linhas me impedindo de ver o gráfico.
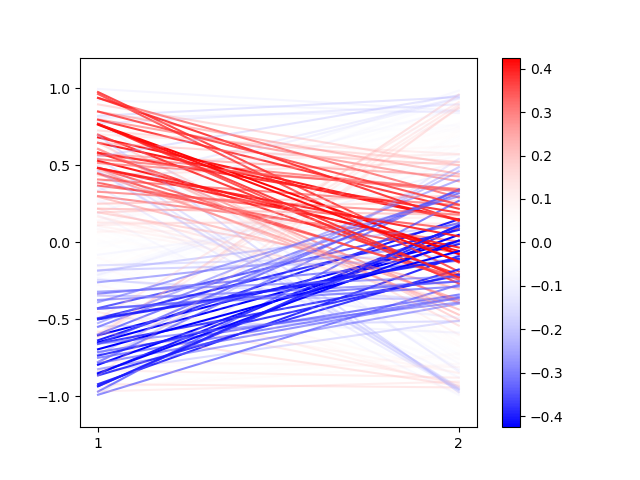
Pode não parecer útil e bem confuso, mas isso só porque estamos olhando em duas variáveis, que de fato a visualização plana é bem melhor. Não despreze porém este gráfico: você consegue ver o padrão oscilatório das linhas em ambos os gráficos, foque nas linhas mais apagadas: de cima para baixo você verá azuis e vermelhas se intercalando. Outra coisa notável é que as linhas se cruzam, com a azuis indo para cima e as vermelhas para baixo. Isso também é consequência do padrão oscilatório.
MUITOS Osciladores harmônicos quânticos
Agora iremos para dezenas de variáveis, e infelizmente a humanidade só consegue racionalizar no máximo um espaço de quatro dimensões. Mas não se preocupe, essa visualização de linhas vai ser bem útil agora, pois todos as dimensões estarão paralelas uma a outra, e você ainda verá claramente para quais “pontos” N-dimensionais (representados pela linha) o estado $\psi$ terá valores mais próximos de zero ou não.
Antes, deixemos claro o que estaremos calculando. Será $N$ osciladores harmônicos quânticos não acoplados, ou seja, que não interagem entre si. Como disse Tom Lancaster, imagine um oscilador no seu quarto, outro no banheiro, etc. Eles não interagem e são separados e não relacionados um do outro, mesmo que nós listemos todos eles em um único vetor $\psi$.
$$ \hat{H} = \sum_n \frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega^2 \hat{x}_n^2 $$
$$ \psi_{\nu_1, \nu_2, \ldots} = \prod_i \psi_{\nu_i} $$
As linhas ainda têm a cor representada pelo valor de $\psi$, e cada ponto agora é representado por uma linha que passa por cada valor de $x_n$.
Podemos fazer por exemplo o gráfico do estado mais básico possível, o $\psi_{0,0,\ldots}:$
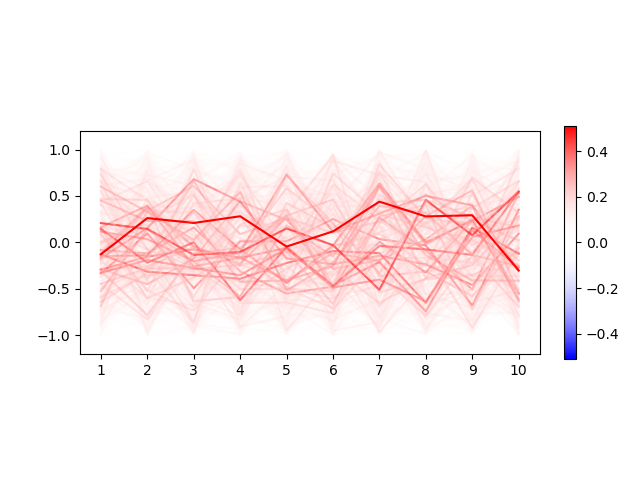
Fascinante. Vamos parar um pouco para analisar o que está sendo desenhado aqui: nós temos $N$ OHQ’s, todos com o nível de energia zero. Então, faz sentido que o valores de $\psi$ mais altos (os mais vermelhos) são linhas que giram em torno da linha $\vec{x}_n = 0$. Mas nossa velha questão de probabilidade na mecânica quântica ainda permite outros estados estados assumirem valores não nulos, mesmo que não sejam exatamente $\vec{x} = \vec{0}$, porém quanto mais distante de $\vec{0}$, menor o valor de $\psi$.
No limite do contínuo
O gráfico acima foi para 10 parâmetros. Mas podemos continuar aumentando esses parâmetros, e pensando que esses osciladores estão ficando cada vai mais próximos um do outro. No limite, ao invés de unidades discretas de parâmetros $\hat{x}_n$, teriamos os infinitos $\hat{\phi}(x)$, como se houvesse um OHQ para cada ponto no espaço. Assim, finalmente podemos interpretar o campo quântico:
Este campo é quântico. De fato, OHQ são quânticos, ou seja, admitem valores discretos de energia: você pode ter $\psi_0 = |0\rangle$, e adicionar uma (1) excitação com energia, $a^\dagger\psi_0 = \psi_1 = |1\rangle$. Isso funciona muito bem para nós, afinal, partículas também são quânticas: você pode ter 0 partículas $|0\rangle$, ou uma partícula $|1\rangle$.
Logo, partículas podem ser pensadas de fato como uma excitação dos campos. Por exemplo, no caso que acabei de fazer o gráfico de $\psi_{0,0,\ldots}$, esse estado assumia valores maiores (ou seja, maior probabilidade de ser o que observamos), quando o campo era (próximo de) $\vec{x} = \vec{0}$. Isso é o mesmo que dizer que o $\psi_{0,0,\ldots}$ corresponde aos valores (próximos de) $\hat{\phi}(x) = 0$.
Da mesma forma que a mecânica quântica admitia várias posições $x$ para um partícula, com $\psi$ dizendo a probabilidade de cada posição, a Teoria Quântica de Campos admite vários possíveis campos $\hat{\phi}(x)$ para um sistema, com $\psi$ nos dizendo a probabilidade de encontrar nosso sistema naquele campo em partícular, e é isso que foi plotado acima.
Como disse no post anteriormente, estado $\psi$ e campo $\phi$ estão intimamente ligados, então não tente racionalizar um sem o outro.
Uma correção
Antes de explorarmos mais estes gráficos de campos quântico, vamos parar um pouco. Nós queremos uma teoria de campos quânticos, e os campos quânticos são como uma cama de mola: se eu aplico uma pertubação em algum lugar dela, essa perturbação se propaga pela cama, como uma partícula se propaga pelo espaço. Essa analogia da cama de molas também nos mostra que uma partícula se propagando pode ser representada por um monte de molas (osciladores harmônicos), porém, diferente de antes, essas molas precisam interagir umas com as outras para que haja a propagação. Isto é, se eu quero construir um hamiltoniano que simule um campo quântico, esses OHQ devem ser acoplados, ou seja, deve ter um termo a mais para essa energia extra:
$$ \hat{H} = \sum_n \frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega^2 \hat{x} _ n^2 + \frac{1}{2}\gamma(\hat{x} _ n - \hat{x} _ {n+1})^2 $$
Mas não se preocupe! Esse termo pode sumir com a mágica das transformações de fourier. Se escrevermos uma transformação de fourier em termo de uma variável $k$ (que você verá que corresponde ao número de onda angular). A transformação de fourier é basicamente uma soma de ondas $X_k$ (neste caso complexas), cada uma com seu número de onda $k = {-\frac{N-1}{2}, \ldots, \frac{N-1}{2}}$:
$$ \hat{x}_n = \frac{1}{\sqrt{N}}\sum_k X_k e^{\frac{-2\pi i}{N} k n} $$
Por razões matemáticas que eu não vou explicar (leia o artigo original se quer detalhes), essa transformação deixa seu hamiltoniano sem esse termo de acoplamento, porém, agora ele depende não mais dos $x_n$ mas sim de $X_k$, e será dado por um hamiltoniano muito similar ao que tinhamos antes de adicionar o acoplamento de OHQ:
$$ \hat{H} = \sum_k \frac{P_k^2}{2m} + \frac{1}{2}\omega_k X_k^2 $$
Onde:
$$ \omega_k = 2\omega \left|\sin\frac{\pi k}{N}\right| $$
$$ P_k = \frac{1}{\sqrt{N}}\sum_k \hat{p}_k e^{\frac{2\pi i}{N} k n} $$
Cujos auto-estados, dado em função das ondas $X_k$ é:
$$\psi_{\nu_1, \nu_2, \ldots}(\vec{X}) = \prod_k H_{\nu_k}(\sqrt{m\omega_k}X_k) e^{-m\omega_k X_k^2/2}$$
Que eu preciso transformar de volta para uma função dos parâmetros $\hat{x}_n$ com uma transformação de fourier inversa.
Um detalhe que irei ignorar aqui é que na verdade existe outra transformação, pois $X_k$ é um número complexo, e nós queremos números reais. Este porém é um trabalho que concerne apenas a mim, e não mudará como deve ser interpretado o gráfico. Para os detalhes, leia o artigo.
Ou seja, os $\psi$ que estavamos olhando anteriormente não iriam descrever os reais campos quânticos. No caso do $\psi_0$ que eu fiz o gráfico, por acaso eles coincidem pois ambos são zero, mas de resto, iriam dar resultados estranhos. Os verdadeiros $\psi(\vec{x})$ que são análogos a um campo quântico (chamamos de “phonons”) são dados pela transformação de fourier inversa do $\psi(\vec{X})$ dado acima.
Enfim, tendo tudo isso em mente, finalmente podemos mostrar os gráficos bonitos.
Acho que farei um post separado para isso, aguarde.