Neste post iremos adentrar um pouco no cálculo numérico. Sabe, você não vai calcular integral na mão toda a vez. Na verdade, muitas das vezes é impossível, e mesmo quando é possível, não ajuda muito.
É muito simples na verdade.
Derivadas
A derivada de uma função $f(x)$ é definida como:
$$ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} $$
Basicamente, o $\frac{\Delta y}{\Delta x} $ com a diferença tendendo a zero. Mas, um computador não consegue calcular limites pois é incapaz de compreender infinito. Eles são porém capazes de calcularem números bem próximos de zero, então isso nos dá uma aproximação de $f’(x)$:
$$ f'(x) \approx \frac{f(x+h)-f(x)}{h} $$
Onde $h$ é um número bem pequeno, tendendo a zero. A análise numérica pode nos dizer quão errado é essa aproximação: basta usarmos as séries de taylor para $f(x+h)$:
$$ f(x+h) = f(x) + hf'(x) + \frac{1}{2}h^2f''(x) + \ldots $$
Obtemos, rearranjando os termos:
$$ \frac{f(x+h)-f(x)}{h} - f'(x) = \frac{1}{2}hf''(x) + \ldots $$
O lado esquerdo da equação é a diferença entre a aproximação e o valor real, ou seja, o erro $E$. O teorema de Taylor nos diz que existe algum $\xi$ entre $x$ e $x+h$ tal que:
$$ \frac{1}{2}hf''(x) + \ldots = \frac{1}{2}hf''(\xi) $$
O que significa que o erro $E$ é dado por:
$$ E = \frac{1}{2}hf''(\xi), \quad \xi \in [x, x+h] $$
Portanto, o maior erro possível dentro de intervalo $[a,b]$ é:
$$ E_{\text{max}} = \frac{h}{2}\max_{x \in [a,b]}(f''(x)) $$
Logo, o valor de $h$ que você deve escolher dado um máximo erro aceitável é:
$$ h = \frac{2E_{\text{max}}}{\max_{x \in [a,b]}(f''(x))} $$
Um outro método (que não irei entrar em detalhes, mas a aproximação é bem óbvia) nos dá:
$$ f'(x) \approx \frac{f(x+h)-f(x-h)}{2h} $$
$$ E_{\text{max}} = \frac{h}{6}\max_{x \in [a,b]}(f''(x)) $$
Aplicando
Digamos por exemplo que eu queira computar uma boa aproximação de $\frac{d}{dx}\sin(\cos(x))$. O erro máximo que aceitarei é de $10^{-6}$. Como consequência da regra da cadeia:
$$ (f \circ g)'' = f''(g(x)) g'(x)^2 + f'(g(x))g''(x) $$
A derivada e segunda derivada de $\sin$ e $\cos$ tem sempre valor (absoluto) máximo $1$. Logo, podemos garantir que $\frac{d^2}{dx^2}\sin(\cos(x)) \leq 1\cdot 1^2 + 1\cdot 1 = 2$. Portanto:
$$ h \leq \frac{2 \cdot 10^{-6}}{2} = 10^{-6}$$
Logo, se $h = 10^{-6}$, o erro não excederá $10^{-6}$. Os valores poderiam ser diferentes, aqui foi uma mera coincidência serem iguais.
Vamos colocar isso tudo numa máquina. Usarei a linguagem python. Primeiro, criarei uma função de derivada, que recebe uma função $f$ e retorna sua derivada $\text{d}f$, usando nossa aproximação:
def D(f):
h = 1e-8
def df(x):
return (f(x+h)-f(x))/h
return df
Então, façamos um gráfico com o matplotlib:
import numpy as np
import matplotlib.pyplot as plt
def D(f):
h = 1e-8
def df(x):
return (f(x+h)-f(x))/h
return df
def f(x):
return np.sin(np.cos(x))
X = np.linspace(-np.pi, np.pi, 500)
Y = [D(f)(x) for x in X]
plt.plot(X, Y)
plt.show()
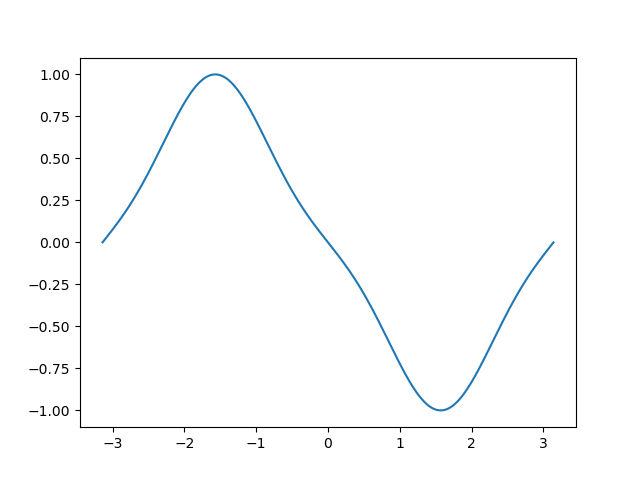
O valor real da derivada é $-\sin(x)\cos(\cos(x))$. Se fizermos agora o gráfico da diferença entre minha aproximação do código com o valor real, temos:
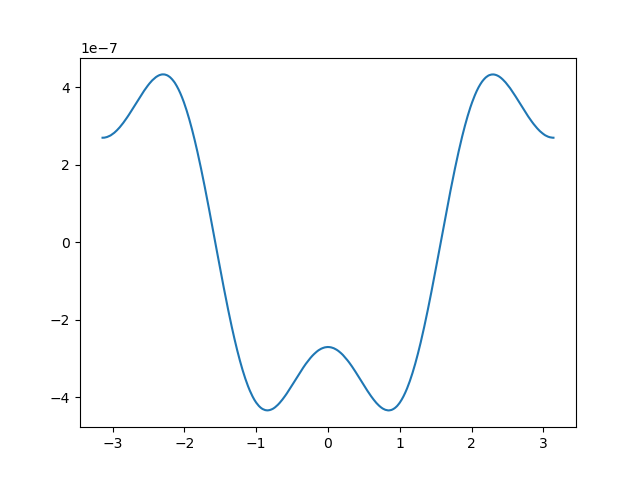
o gráfico nos diz que o maior erro é $\approx 4 \cdot 10^{-7}$, que de fato é menor que $10^{-6}$.
Tome cuidado! Você não pode usar números extremamente pequenos e esperar que o resultado seja melhor ainda. O problema é que os números tem um limite do quão pequeno pode ser um número (pesquise por “Épsilon de máquina”). Isso significa que, ao computar o $\frac{\Delta y}{\Delta x}$, ambos os $\Delta$ vão acabar sendo igual ao épsilon da máquina, que é basicamente o menor número possível para o computador, e então teremos $\frac{\Delta y}{\Delta x} = 1$.
Segunda derivada
O mesmo processo de aproximação pode ser feito:
$$ f''(x) \approx \frac{f'(x+h)-f'(x)}{h} $$ $$ \approx \frac{\frac{f(x+h)-f(x)}{h}-\frac{f(x)-f(x-h)}{h}}{h} $$ $$ = \frac{f(x+h) + f(x-h) - 2f(x)}{h^2} $$
E usando as séries de taylor de $f(x+h)+f(x-h)$, obtemos:
$$ f(x+h)+f(x-h) = 2f(x) + h^2f''(x) + \left[ \frac{1}{12}f^{(4)}(x) + \ldots \right] $$
Isolando o $f''(x)$, temos que o erro $f''(x) - \frac{f(x+h) + f(x-h) - 2f(x)}{h^2}$ é:
$$ E = \frac{-1}{12} h^2 f^{(4)}(\xi), \quad \xi \in [x, x+h] $$
Integrais
As integrais são bem mais fáceis. Lembre-se do conceito básico, as integrais são as somas de vários retângulos de base $dx$ e altura $f(x_n)$. A questão é que é preciso tomar o limite em que o número de retângulos tende ao infinito. Aqui, apenas diremos que $N$ é um número bem grande:
$$\int_a^b f(x) dx \approx h\sum_{n=0}^N f(a + hn)$$
Onde $h = \frac{b-a}{N}$ é o nosso $dx$. Podemos tirar o $h$ para fora do somatório pois assumimos que todos os retângulos estão igualmente espaçados.
A questão é que existe uma aproximação melhor dada pela regra do trapezóide, que apesar de parecer diferente, que envolve tirar a mediana da função entre dois pontos, na prática você precisa pegar a mediana dos dois pontos nos extremos e os do meio são somados igual antes:
$$\int_a^b f(x) dx \approx h\frac{f(a)+f(b)}{2} + h\sum_{n=1}^{N-1} f(a + hn)$$
O $h$ novamente pode (e deve) ser fatorado na hora de computar no computador.
A análise de erro aqui é mais chatinha de explicar, caso queira detalhes consulte um livro (recomendo “Numerical Mathematics and Computing”, e para a galera do tapa-olho e papagaios, procure por Library Genesis na net). Enfim, aqui o erro:
$$ E = \frac{-1}{12} (b-a) h^2 f''(\xi)$$
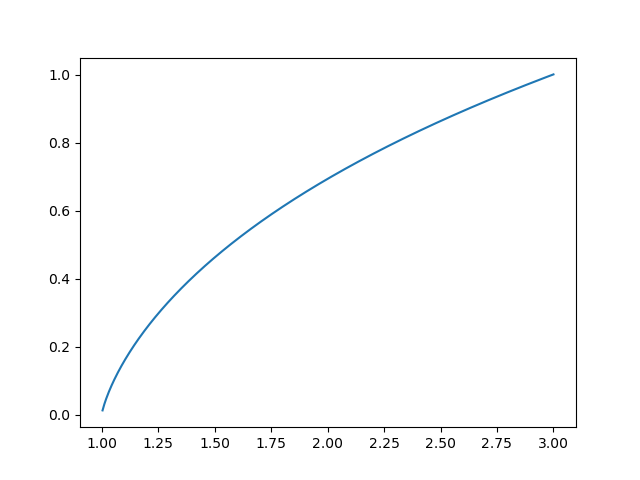
Um exemplo de implementação em python, integrando $\frac{1}{x}$ (e obtendo $\ln(x)$):
import numpy as np
import matplotlib.pyplot as plt
def integral(f, a, b, N = 1000):
h = (b-a)/N
s = (f(a) + f(b)) / 2
for x in np.linspace(a+1, b-1, N):
s += f(x)
s *= h
return s
def f(x):
return 1/x
X = np.linspace(1, 3, 500)
Y = [integral(f, 1, x) for x in X]
plt.plot(X, Y)
plt.show()
Equações diferenciais, método de Euler
Agora entra a parte divertida, resolver equações diferenciais. Diferente de derivadas e integrais, as equações sempre foram meio “misteriosas”, no sentido que é difícil ver o que é a solução dela, sem passar um tempo quebrando a cabeça com métodos malucos de resolver. O fato é que na prática dificilmente alguém vai resolver essas equações na mão. Ou o sujeito usa um site como wolframalpha.com , ou ele resolve numericamente. Aqui, faremos o segundo.
O princípio do método de Euler é trocar os $dx$, $dy$ por variações explícitas $\Delta x$ e $\Delta y$. Na verdade, foi isso que fizemos para cálcular as derivadas. Nosso $\frac{dy}{dx}$ virou $\frac{\Delta y}{\Delta x}$, porém se o $\Delta x$ é um número $h$, então o $\Delta y$ é $f(x+h)-f(x)$.
Para o método de Euler, iremos análisar cada “instante” da equação numa lista (ou posteriormente em matrizes). Ou seja: $y(x) = y_n$, e o próximo instante é o próximo item da lista: $y(x+h) = y_{n+1}$. Nessa notação, as derivadas que tinhamos antes viram:
$$ y'(x) \approx \frac{y_{n+1} - y_n}{h}$$
$$ y''(x) \approx \frac{y_{n+1} + y_{n-1} - 2y_n}{h^2}$$
Isso é muito útil para resolver derivadas quando sabemos algum valor inicial, e queremos ir computando os próximos valores da lista passo a passo.
O princípio básico é substituir as derivadas pelas aproximações e isolar $y_{n+1}$. Por exemplo:
$$y' = f(x, y)$$
$$\frac{y_{n+1} - y_n}{h} = f(x_n, y_n)$$
$$y_{n+1} = y_n + hf(x_n, y_n)$$
O número de etapas é claro será determinado pelo $h$. Se, por exemplo, quero resolver o problema com um valor inicial $y(0)$ conhecido até $y(2)$, e $h = 0.001$, então $y(1) = y_{2000}$, já que preciso de 2000 passos de tamanho $0.001$ para sair de $x=0$ até $x=2$. Isso pode ser dito também que para o cálculo com precisão $N = 2000$, $h = 0.001$.
Um exemplo de código, iremos resolver $y' = -xy$, com o valor inicial $y_0 = y(-3) = 0.0111$ até o valor $y(3)$, e uma precisão $N=1000$:
import numpy as np
import matplotlib.pyplot as plt
N = 1000
X = np.linspace(-3, 3, N)
h = 6/N
Y = np.zeros(N)
Y[0] = 0.0111
def f(x, y):
return -x*y
for n in range(N-1):
Y[n+1] = Y[n] + h*f(X[n], Y[n])
plt.plot(X, Y)
plt.savefig("diffeq.png")
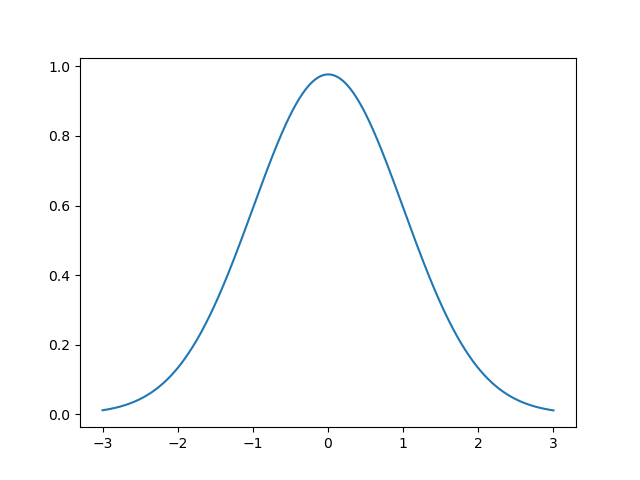
Tcharam! A resposta é um curva gaussiana, e eu não precisei fazer continha nenhuma. Melhor: nosso código funciona para qualquer $f(x, y)$ e condições iniciais que eu botar.
Equações diferenciais parciais
E é claro que esse método funciona para EDP também. Mas dessa vez, ao invés de escrever $h$, eu vou escrever $\Delta x$ ou $\Delta y$, dependendo de qual derivada estou analisando. Isso porque cada variável tem sua precisão.
É mais fácil explicar com um exemplo. Peguemos nossa equação de calor:
$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x}$
Eu vou assumir que $\alpha = 1$, e não lidarei com mais variáveis espaciais pois quero mostrar num gráfico do matplotlib).
Podemos fazer a boa e velha troca de derivadas para suas aproximações:
$\frac{u_{n_{t+1}} - u_{n_t}}{\Delta t} = \frac{u_{n_{x+1}} + u_{n_{x-1}} - 2u_{n_x}}{\Delta x^2}$
A notação correta seria $u_{n_t, n_x}$, e, por exemplo, a derivada: $\frac{u_{n{t+1}, n_x} - u_{n_t, n_x}}{\Delta t}$, pois a função não depende apenas de uma variável, o que reflete o fato que na computação, eu vou ter que fazer um loop que varie por todos os valores de $x$, e computar a derivada em cada um deles.
Mas por questões estéticas, mostrarei o índice somente da variável sendo variada durante a derivada.
Assumiremos que temos todos os valores espaciais de $u$ no tempo inicial, e queremos prever como a função evolui com o passar do tempo. Portanto, isolamos $u_{n_t+1}$:
$$u_{n_{t+1}} = u_{n_t} + \frac{\Delta t}{\Delta x^2}\left( u_{n_{x+1}} + u_{n_{x-1}} - 2u_{n_x} \right)$$
No ponto de vista da programação, ao invés de uma lista com cada instante do $y$, teremos uma matriz, onde cada “dimensão” da matriz refere a uma variável. Então, por exemplo, $u_{n_t, n_x}$ é u[nt][nx]. Assim, vamos preencher uma coluna da matrix por iteração.
Para cada variável teremos uma precisão, por exemplo: $N_t$, $N_x$.
Continuando com o exemplo, suponha que eu tenha dado como valor inicial $u(0, x)$ para todos os pontos $x$. Quero ver a evolução dessa função indo até $u(0.5, x)$. Os valores iniciais serão uma curva gaussiana pontuda, a precisão do tempo $N_t$ será $120$ e a precisão espacial $N_x = 100$. A função estará delimitada em $-3< x < 3$.
import numpy as np
import matplotlib.pyplot as plt
Nt = 120*100
Nx = 100
T = np.linspace(0, 0.5, Nt)
X = np.linspace(-3, 3, Nx)
U = np.zeros([Nt, Nx])
dt = 0.5/Nt
dx = 6/Nx
# Valor inicial
for nx in range(Nx):
U[0][nx] = 5*np.exp(-25*X[nx]**2)
# Resolver a equação:
for nt in range(Nt-1):
for nx in range(1, Nx-1):
U[nt+1][nx] = U[nt][nx] + (dt/(dx**2)) * (U[nt][nx+1] + U[nt][nx-1] - 2*U[nt][nx])
for nt in range(0, Nt-1, 100):
plt.ylim([0, 5])
plt.plot(X, U[nt])
name = (3-len(str(int(nt/100))))*'0' + str(int(nt/100))
plt.savefig(name+'.png')
plt.close()
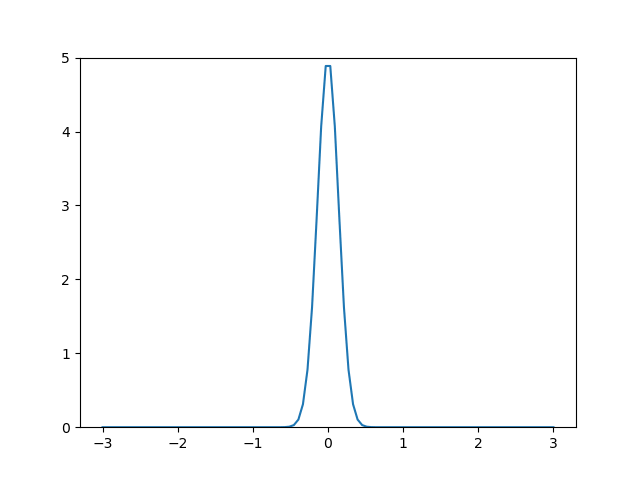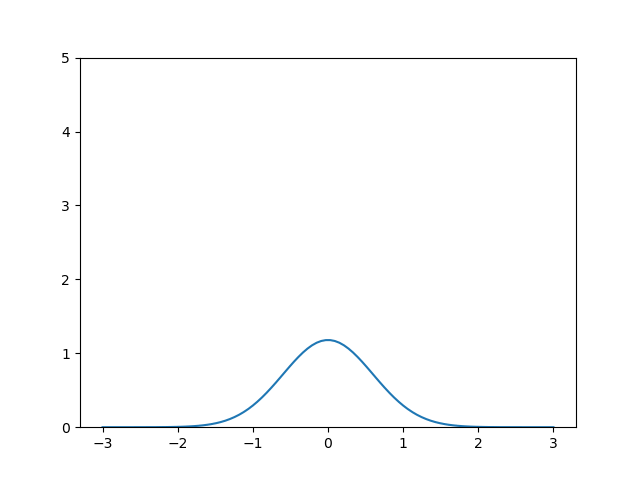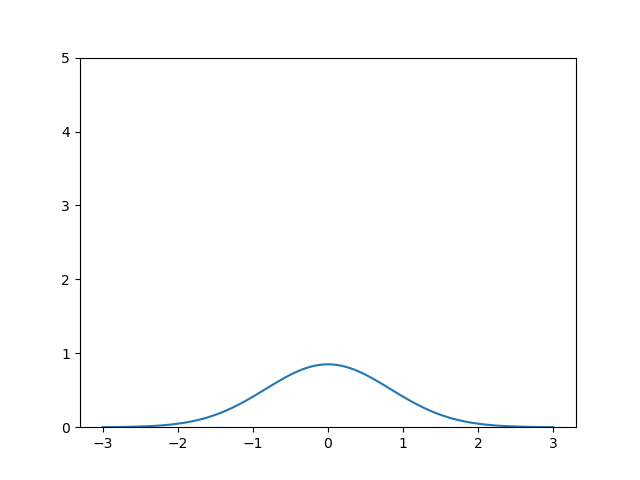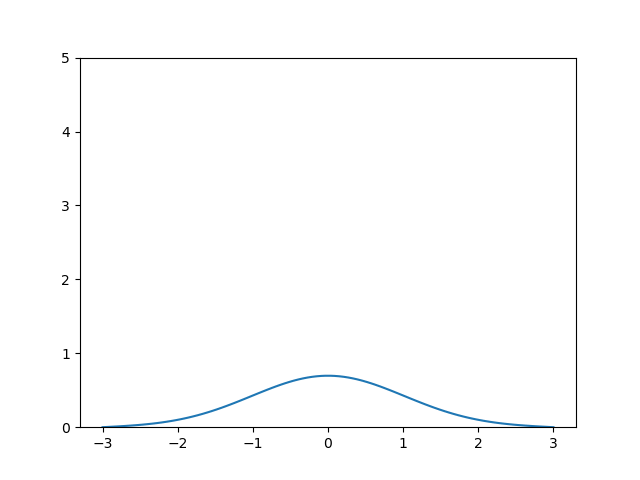
Enfim, é tudo que a tenho a falar por hoje. Em breve, resolvendo equações diferenciais na prática.