Recomendo que tenha um conhecimento básico de análise numérica ou leia o post anterior.
Neste post vou mostrar como se resolve uma equação diferencial com python. Apesar de ser importante saber como faz manualmente os métodos numericos do post anterior, na prática as pessoas apenas usam bibliotecas que fazem tudo isso de forma muito mais eficiente que você jamais consegueria chegar sozinho.
Primeira ordem
Primeiro, com equações diferenciais de primeira ordem, a mais simples de todas é:
$$ y' = f(x) $$
A solução obviamente é apenas uma integral:
$$ y = \int f(x) dx $$
E nesses casos você pode simplesmente pegar sua equação e botar num site como o wolframalpha.com e pegar uma solução analítica. Mas e se sua função $f$ não depender apenas de $x$, mas também de $y$, temos:
$$ y' = f(x, y) $$
Que é a forma mais geral de uma equação diferencial de primeira ordem. No caso, você sempre pode reduzir uma ODE de primeira ordem para este formato. Por exemplo, se $y'$ está alguma em expressão maluca:
$$ \ln(\arcsin(y')) - y\tan{x} = 0 $$
Você pode isolar o $y'$:
$$ \ln(\arcsin(y')) = y\tan{x} $$ $$ \arcsin(y') = e^{y\tan{x}} $$ $$ y' = \sin(e^{y\tan{x}}) $$
Você vai querer reduzir a equação anterior neste formato, que é o formato padrão que as bibliotecas usam para aplicar o método de Euler que vimos no post anterior. Na verdade, as bibliotecas usam métodos mais avançados ainda, como o de Runge-Kutta, que é praticamente uma generalização do método de Euler.
A função milagrosa que fará isso por nós é da biblioteca scipy. Esta biblioteca tem uma gama de funções que resolvem problemas típicos na área da ciência da computação. Por exemplo, resolver equações da algebra linear
, minimização de funções
, entre diversas outras coisas interessantes. Vale checar o guia
para compreender melhor
O solve_ivp resolverá as equações neste formato. IVP significa “Initial Value Problem”, ou o Problema de Valor Inicial, já que existem infinitas soluções para uma equação diferencial, e é necessário o IVP para delimitar uma única solução.
Outra biblioteca que vou usar é o numpy. É basicamente uma biblioteca de matemática cheia de funções muito úteis. O np.linspace(a, b, N) cria uma lista com N números de a até b, igualmente espaçados.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(np.exp(y * np.tan(x)))
t_span = [0, 1.4] # valor inicial e valor final de x
t_eval = np.linspace(0, 1.4, 1000) # lista de x que serão computados os y(x)
y0 = 1 # valor inicial de y
sol = solve_ivp(f, t_span, [y0], t_eval=t_eval,
method='LSODA', rtol=1e-6, atol=1e-12)
plt.plot(sol.t, sol.y[0])
plt.show()
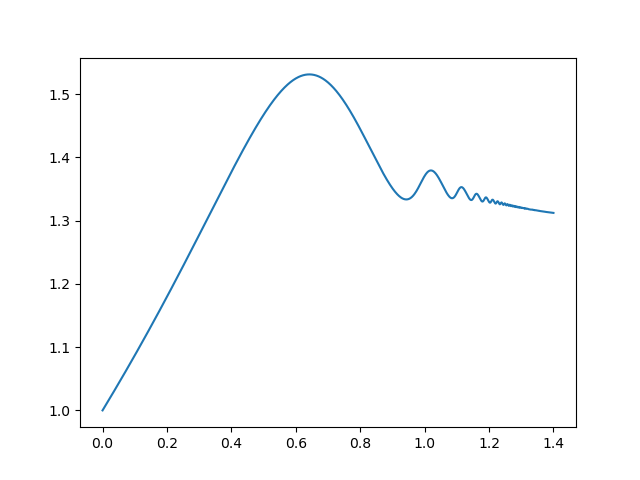
A notação padrão é usar a variável padrão $t$ ao invés de $x$, porque geralmente nos contextos aplicados na prática o $t$ é mais utilizado. Por isso, os nomes t_span e t_eval. Em geral, evite mexer no method, deixe em branco e o programa vai usar o padrão dele. No meu caso em específico foi necessário pois é uma função muito maluca que precisa de um método mais específico (que porém é bem mais lento). Idem para o rtol e atol, que são valores de tolerância de erro.
EDO de segunda ordem (ou pior)
A maioria das equações diferenciais que você lida na prática são de segunda ordem. O problema: o scipy só resolve EDO de primeira ordem.
Se você estudou Equações Diferenciais sabe que tem uma simples solução: toda equação diferenciais de enésima ordem pode ser reduzida a um sistema de equações diferenciais de primeira ordem. Na verdade, um sistema de equações de enésima ordem pode ser reduzido num sistema de primeira ordem.
E a notícia boa é que o solve_ivp resolve sistemas de equação. Não é à toa que o y0 teve que ser botado dentro de uma lista.
Pegue, por exemplo, a equação do pêndulo:
$$ \frac{d^2\theta}{dt^2} = -k\sin(\theta) $$
Onde $k = \frac{g}{l}$, a constante gravitacional pelo comprimento da corda. Podemos transformar em uma equação com duas variáveis, $\theta$ e $\dot{\theta}$. Pense no $\dot{\theta}$ como uma nova variável.
$$ \begin{cases} \frac{d\theta}{dt} &= \dot{\theta} \\ \frac{d\dot{\theta}}{dt} &= -k\sin(\theta) \end{cases} $$
Ou, de forma vetorial:
$$ \frac{d}{dt} \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} \dot{\theta} \\ -k\sin(\theta) \end{bmatrix} $$
Se chamarmos o $[\theta, \dot{\theta}]$ de um vetor $\vec(y)$ e o $[\dot{\theta}, -k\sin(\theta)]$ de uma função $f(t, \vec{y})$, então temos:
$$ \vec{y}' = f(t, \vec{y}) $$
Que é o caso geral que nós tinhamos antes, mas agora decidi colocar a variável “padrão” $t$ ao invés de $x$, e agora temos um vetor $\vec{y}$ ao invés de um número y. O importante é que está no formato do solve_ivp:
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
k = 1
def f(t, y):
theta, theta_dot = y
return [
theta_dot,
-k*np.sin(theta)
]
t_span = [0, 20]
t_eval = np.linspace(0, 20, 1000)
y0 = [np.pi-0.2, 0] # valor inicial do vetor y
sol = solve_ivp(f, t_span, y0, t_eval=t_eval)
plt.plot(sol.t, sol.y[0])
plt.show()
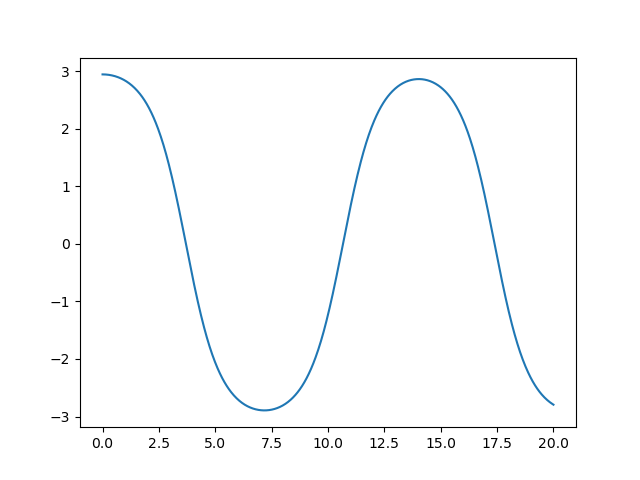
Um exemplo mais complexo que venho trabalhando são as geodésicas. Elas compõe um sistema de equações diferenciais de segunda ordem, mas isso fica para o próximo post.