Como o TRI funciona?
Primeiro, resumindo como o TRI funciona: cada questão possui uma probabilidade de acertar em função da habilidade $\theta$, número este que descreve a proficiência do candidato em determinada área, como Matemática ou Ciências da Natureza. Essa probabilidade é uma função logística determinada por três parâmatros $a$, $b$ e $c$.
$$ P(acertar | \theta) = c + \frac{(1-c)}{1+\exp[-a(\theta-b)]} $$
O parâmetro $a$ é o de discriminação, ela determina o quão bom é essa questão em separar alunos que sabem ($P \approx 1$) e os que não sabem ($P \approx 0$). Na curva, reflete num crescimento acentuado:
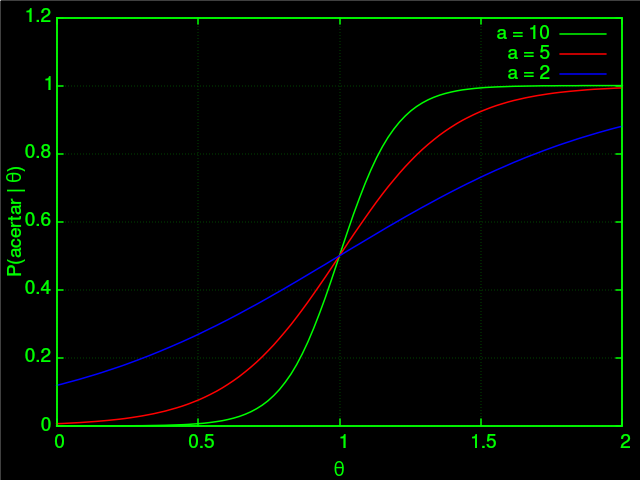
O parâmetro $b$ é o de dificuldade. Na curva, reflete o ponto em que a curva sobe. Ou seja, determina a nota média de corte dos alunos que sabem:
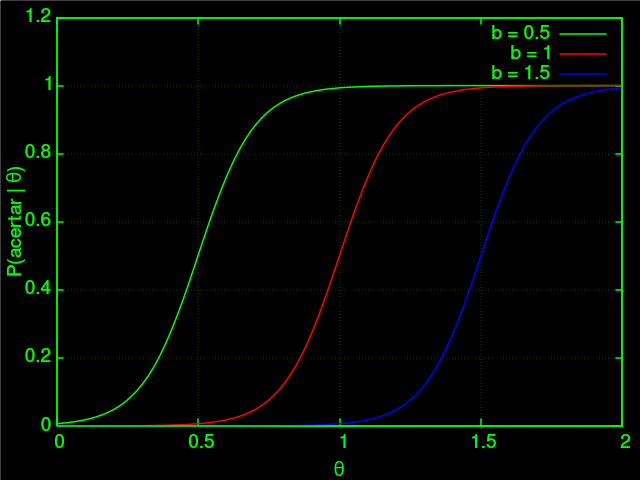
E por fim, $c$ é o parâmatro de assíntota, que descreve basicamente a probabilidade de alguém com habilidade baixa conseguir resolver o problema:
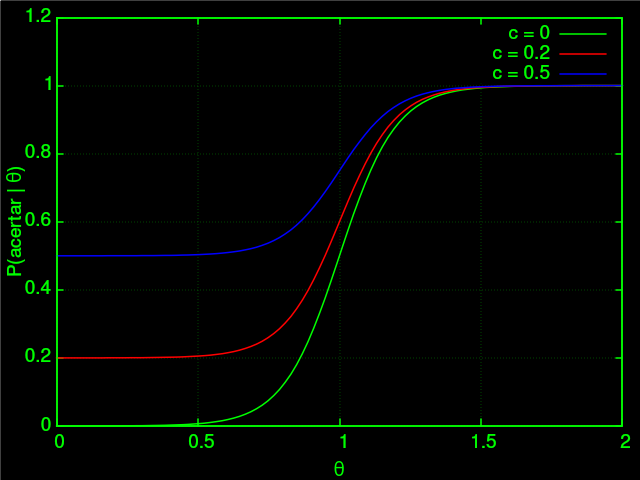
Esses parâmetros de cada questão são obtidos num pré-teste com alunos do terceiro ano do ensino médio. Segundo o INEP, 100 mil estudantes distribuídos por CEP para melhor amostragem. Com esses dados, é possivel fazer uma regressão linear para calibrar os três parâmetros de cada questão.
Depois das provas do ENEM de fato, alguns itens podem ter parâmetros de pré-teste diferentes do reais. Então, eles fazem uma recalibragem dos parâmetros para adequar com os candidatos ao ENEM. Essa última recalibragem é a que será usada nos cálculos de proficiência.
Estatística bayeasiana
O ENEM usa estatística bayeasiana. A ideia é a seguinte: O ENEM sabe qual a probabilidade de acertar alguma questão dada uma proficiência: $P(acertar | \theta)$. O Objetivo agora é obter o inverso: Qual a probabilidade de uma pessoa ter essa proficiência dado os acertos: $P( \theta | acertos)$.
A solução é o teorema de bayes:
$$ P(A | B) = \frac{P(B | A) P(A)}{P(B)} $$
Então aplicando essa fórmula para nosso problema:
$$ P(\theta | acertos) = \frac{P(acertos | \theta) P(\theta)}{P(acertos)} $$
O $P(acertos | \theta)$ é simples: A chance $P_n$ de acertar ou errar uma questão é simplesmente o $[P(acertar_n | \theta)]$ ou $[1-P(acertar_n | \theta)]$ no caso de erro. Então a probabilidade de todos os acertos e erros $P(acertos | \theta)$ é:
$$ P(acertos | \theta) = \prod_n P_n$$
A segunda parte parte é $P(\theta)$, a probabilidade de alguém ter essa proficiência. Estritamente matematicamente falando, é impossível obter uma expressão, e é aí que entra um dos princípios filosóficos bayesianos: nós simplesmente inventamos uma probabilidade, chamada função a priori. No caso, a que mais faz sentido é uma função normal, pois baseado em estudos prévios, as distribuições de habilidade se dão em uma distribuição normal:
$$ P(\theta) = \frac{e^{\frac{-\theta^2}{2}}}{\sqrt{2\pi}} $$
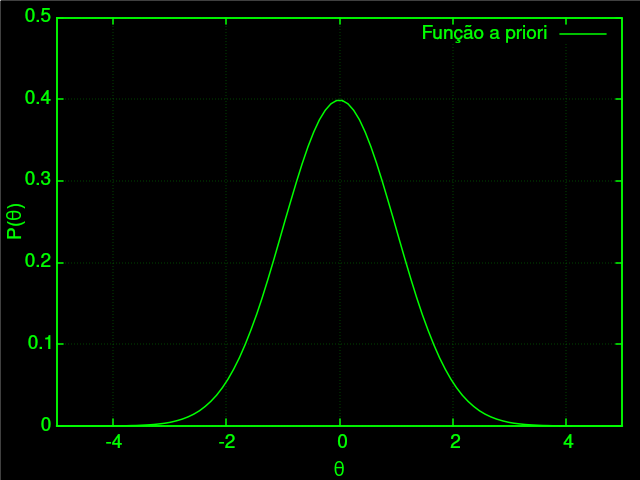
Já a última parte é $P(acertos)$, basicamente, a probabilidade de alguém aleatório acertar/errar essas exatas questões. A ideia é simplesmente integrar sobre o produto $P(acertos | \theta)P(\theta)$, pois esta será a probabilidade de alguém ter a proficiência $\theta$ e acertar as determinadas questões. Depois integramos sobre todas as possibilidades.
Assim, a expressão que obtemos é:
$$ P(\theta | acertos) = \frac{P(acertos | \theta) P(\theta)}{\int_\mathbb{R}P(acertos | \theta) P(\theta) d\theta} $$
A nota do ENEM então é obtida por:
$$ EAP(\theta | acertos) = \frac{\int_\mathbb{R}\theta P(acertos | \theta) P(\theta)d\theta}{\int_\mathbb{R}P(acertos | \theta) P(\theta) d\theta} $$
$$= \frac{\int_\mathbb{R}\theta \left(\prod_n P_n\right) \frac{e^{\frac{-\theta^2}{2}}}{\sqrt{2\pi}}d\theta}{\int_\mathbb{R}\left(\prod_n P_n\right) \frac{e^{\frac{-\theta^2}{2}}}{\sqrt{2\pi}} d\theta}$$
Ok. Muita coisa para compreender. O $EAP(\theta | acertos)$ é, essencialmente, o valor esperado do $\theta$, sua proficiência naquela área, dado suas respostas (o “acertos”).
Para deixar claro o que está ocorrendo: cada proficiência $\theta$ tem uma certa probabilidade associada com ela, que é o $P(acertos | \theta)$, que eu vou chamar de $L$, do inglês likelihood. Digamos que eu acertei algumas 30 questões da prova; qual a probabilidade de alguém com proficiência $0$ ter acertado 30 questões? Muito baixa, então $L \approx 0$. Qual a probabilidade de alguém com proficiência $1000$ acertar só 30 questões? Também baixa, então também $L \approx 0$. Agora uma pessoa com proficiência $700$ tem alta probabilidade de acertar essas 30 questões (e errar as outras).
A expressão $EAP(\theta | acertos)$ é, como eu disse antes, o valor esperado de $\theta$. Então cada $\theta$ tem uma probabilidade, e nós pegamos o valor mais provável, quem já estudou estatística vai reconhecer isso na integral.
Outro efeito disso é que evitar chutes: você errou várias questões fáceis e acertou uma difícil, quanto ela vai “valer” na sua nota? A probabilidade de alguém com proficiência alta acertar a questão é de fato alta, mas esse valor será ofuscado no produto com as várias questões fáceis que você errou, porque alguém com proficiência alta não erraria elas. Então ela não ira contribuir muito para $L$ em valores altos (mas ainda vai valer mais do que marcar ela errado, é claro).
Essas proficiências $\theta$ estarão numa distribuição normal com média $0$ e desvio padrão $1$. Então, para obter sua nota real naquela área, é preciso fazer a conversão:
$$ \textbf{Nota} = 100EAP + 500 $$
Para que a média seja $500$ e a desvio padrão seja $100$
Por exemplo, assumindo que todas as questões tenham o mesmo parâmetro:
$$ P(acertar | \theta) = 0.1 + \frac{0.9}{1+\exp[-2\theta]} $$
Se eu acertei, digamos, $30$ questões e errei $15$:
$$ P(acertos | \theta) = P(acertar | \theta)^{30}(1-P(acertar | \theta))^{15} $$
Então $EAP \approx 0.3$, e a minha nota será $530$. Se eu acertasse todas as $45$, minha nota seria $773$. Aqui um gráfico com a relação de notas e pontuação, assumindo a probabilidade igual pra todas:
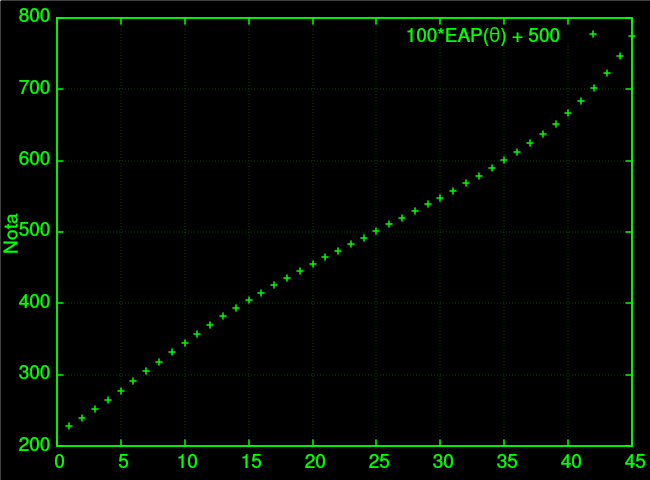
(Caso você seja uma pessoa infeliz que não entendeu o que eu disse, pode ler o próprio artigo do INEP que fala a mesma coisa que eu: https://download.inep.gov.br/publicacoes/institucionais/avaliacoes_e_exames_da_educacao_basica/enem_procedimentos_de_analise.pdf )
Estimando notas
Quero estimar minha nota do ENEM. Problema: é impossível eu obter os parâmetros de cada questão para eu calcular. Apesar disso, é fato que em geral as notas do ENEM por pontuação são mais ou menos consistentes: uma pessoa que acerta $30$ questões em humanas vai tirar $600 - 700$.
Nosso método será simples: obter um intervalo de confiança de 99% para a nota do enem.
Como visto anteriormente, a relação a nota de uma pessoa, dada uma certa pontuação, segue uma distribuição padrão. Isso simplifica nossos cálculos: vamos criar uma distribuição padrão que seja a média de, digamos, os últimos 5 anos do enem.
Por exemplo, se as médias de notas de 2020, 2021 e 2022 para quem acertou $39$ questões sejam $880$, $910$, $900$, então a média das três seria $\approx 896$. Então se eu acertei $39$ questões em 2023, mesmo eu não sabendo nenhum dado da prova desse ano, eu posso estimar que vou tirar uma nota próxima de $896$.
Mas não basta apenas obter a média. Como eu disse antes, eu quero um intervalo de notas, que eu tenha 99% de certeza de que minha nota vai cair dentro deste intervalo. Isso significa obter o desvio padrão $\sigma$ e calcular o intervalo $896 - 2.56\sigma, 896 + 2.56\sigma$ ($2.56$ é o número para um intervalo de 99% de confiança).
Como vamos obter os dados? Bom, o INEP na verdade libera todos os dados: https://www.gov.br/inep/pt-br/acesso-a-informacao/dados-abertos/microdados/enem
Baseado nisso podemos obter milhares de coisas. Por exemplo, aqui eu extrai a relação de pontuação e nota do enem em matemática de 1000 candidatos:
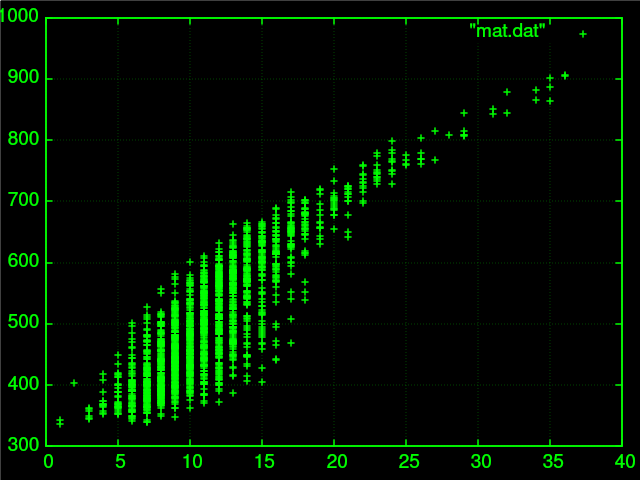
Veja que esse gráfico segue uma certa tendência, e que cada pontuação ($0-45$) tem sua nota média ($0-1000$) crescendo de forma linear. O desvio padrão de pontuações mais baixas é alto, enquanto para pontuações maiores é baixa.
Podemos compilar todos esses dados num gráfico mais compacto:
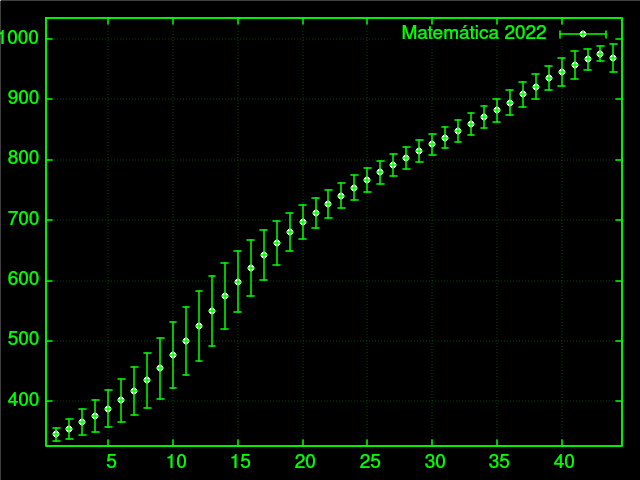
Basta agora pegar essas notas médias e usar como meus dados para 2023? Claro que não, porque cada ano as médias podem mudar. Por exemplo, 2022 teve uma média de notas consideravelmente mais alta que 2021:
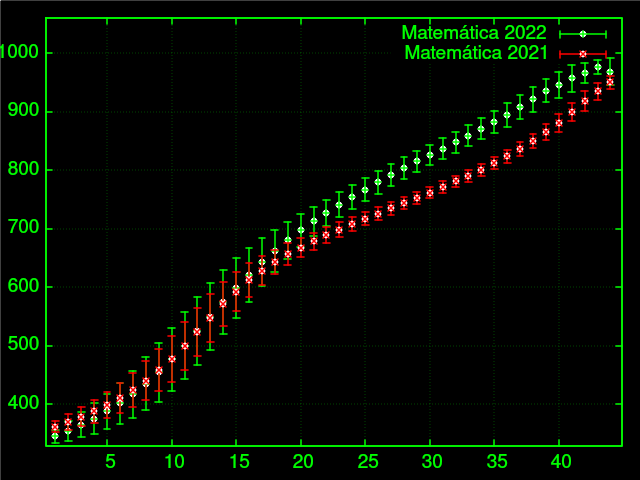
Os conhecidos da estatística reconhecem que este é o velho problema do teorema central do limite. Podemos dizer que cada ano $n$ é uma amostra com média $\bar{x}_n$ e desvio padrão $s_n$. Essas médias e desvios padrão estão “próximos” da média “verdadeira” $\mu$ e desvio $\sigma$. O teorema então nos vai dizer que
$$ \mu \approx \frac{\sum_n^N \bar{x}_n}{N} $$
E
$$ \sigma \approx \sqrt{n}s_{\bar{x}} $$
Onde $s_{\bar{x}}$ é o erro padrão, ou seja, o desvio padrão das médias amostrais com a média “verdadeira”:
$$ s_{\bar{x}} = \sqrt{\frac{\sum_n^N (\mu - \bar{x}_n)^2}{N}} $$
O que eu fiz então foi obter dados dos últimos 5 anos e aplicar as fórmulas anteriores. Dessa forma, obtemos uma média aproximada e desvio aproximado para 2023, o que nos permitirá criar intevalos de confiança em torno da média. Por exemplo, para matemática temos:
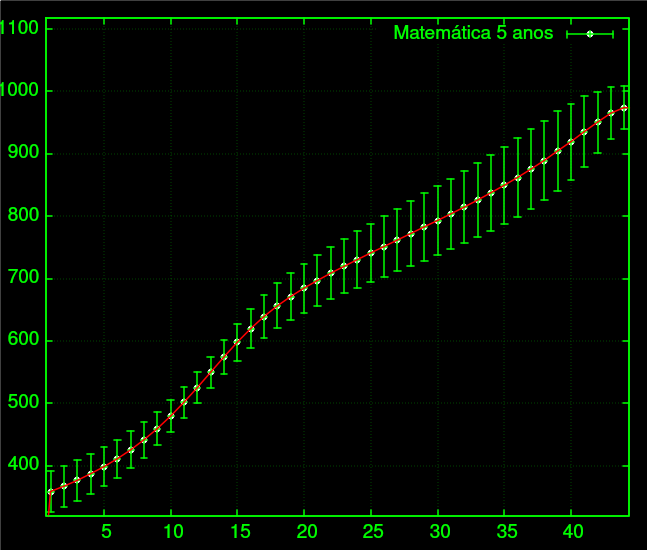
O desvio padrão é alto, e esse é o preço a se pagar pela certeza da nota.
Calculadora
Compilando todos os dados que eu obtive, eu fiz uma calculadorazinha bem simples que obtém sua média provável para 2023 baseado em suas notas, e um intervalo de confiança, que por padrão é $90%$. Também aproveitei e coloquei uma calculadora de média ponderada que merece um pouco de explicação:
A média ponderada é essencialmente uma combinação linear das distribuições padrão de cada ano. A soma dessas quatro (cinco com a redação) variáveis aleatórias será também uma variável aleatória, e como todas são normais, a média ponderada também será uma distribuição normal. Os web-livros nos informam que a média dessa distribuição será, obviamente, a média ponderada das outras distribuições:
$$\bar{X} = \frac{p_1\mu_1 + p_2\mu_2 + p_3\mu_3 + p_4\mu_4 + p_5\mu_5}{p_1+p_2+p_3+p_4+p_5} $$
E o desvio padrão:
$$ \sigma_{\bar{X}} = \sqrt{\sum_{n=1}^5\left(\frac{p_n}{p}\sigma_n\right)^2} $$
Onde $p = p_1+p_2+p_3+p_4+p_5$ é a soma de todos os pesos.
Link: https://muriloucolouco.github.io/calculadora