Matemática do mercado financeiro

January 28, 2025 - 7 mins read

Em compensação do post anterior, este será dedicado a introduzir a matemática por trás de toda a análise, devidamente justificada e explicada através de estudos cientificos.

Benoit Mandelbrot e a natureza fractal do mercado

Você com certeza já ouviu falar no Conjunto de Mandelbrot, exemplo da beleza matemática. O que poucos sabem é que o mesmo cara responsável por esse conjunto também foi um grande estudioso do mercado finaceiro, especificamente sobre a teoria da rugosidade e fractal que os gráficos de preços de ações e outros ativos financeiros possuem.

Dizer que algo é fractal é basicamente dizer que esse algo tem comportamento complexo e “rugoso” não importa o quão próximo você chegue do gráfico (sim, nem todo fractal é repetitivo). O conjunto de mandelbrot é um dos exemplos mais famosos disso:

Zoom no Conjunto de Mandelbrot

Porém, esse comportamento também aparece nos preços de ativos financeiros. Seja colocando o time span das velas para 1 minuto, 1 hora, 1 dia, os gráficos sempre são “rugosos”, cheios de altos e baixos, não tem como saber qual o tempo passado só de olhar para o formato do gráfico:

(Preços do PETR4, clique para maior resolução)

Isso nos indica que os gráficos são formados por tendências de várias escalas:

Tendências grandes a longo prazo (por exemplo, o aumento de compra de GPU por conta de IA, fazendo com que as ações da NVIDIA aumentassem ao numa escala de anos).
Tendências médias a médio prazo (Como o lançamento da deepseek, desestabilizando as ações da NVIDIA e fazendo ela cair o preço).
Tendências pequenas a curto prazos (Tipo um investidor colocando muito dinheiro numa empresa).
Tendências minúsculas em instântes (Você colocando seus 100 reais numa ação da OIBR3 achando que vai ficar rico).

Tudo isso acontece dentro de um sistema extremamente complexo chamado sociedade. A maiorias dos efeitos são pequenos, mas mais raramente, grandes eventos acontecem que criam tendências grandes.

Modelo estocástico

Como (ainda) é impossível simular a humanidade inteira dentro de um computador, para efeitos práticos, cada um desses eventos podem ser considerados aleatórios. Claro, não são genuinamente aleatórios, mas a complexidade humana cria um caos o suficientemente parecido com aleatoriedade.

Isso é similar ao movimento browniano: um átomo descreve um movimento aparentemente aleatório. Isso ocorre porque existe milhões de partículas interagindo entre si de forma complexa e imprevisível, fazendo com que o átomo se mova de forma efetivamente randômica.

Essa mesma ideia será usada para nossa primeira forma de modelar os preços de ativos no mercado. Chamaremos o preço de um ativo financeiro em um determinado instante $t$ de $S(t)$. O que queremos saber é a variação $dS$ após se passar um instante $dt$.

Se pautando no que foi dito anteriormente (de contribuições grandes serem mais raras que as contribuições pequenas), podemos definir uma variação aleatória normalmente distribuída:

$$ dW \sim N(0, dt) $$

Distribuição normal

Isso significa dizer que a variação aleatória $dW$ tem média $0$, e desvio padrão $dt$. Ter desvio padrão $dt$ significa que 68% dos valores de $dW$ estarão entre $-dt$ e $dt$, e 95% estarão entre $-2dt$ e $2dt$, e variações maiores serão mais raras.

Porém, além da variação $dW$, vamos ter que:

$dS$ precisa ser proporcional a $S$. Ou seja, se $S(t) = 1.00$ e ele variou $0.01$, então quando $S(t) = 10.00$, você esperará que ele varie $0.10$.
Uma constante de ajuste $\sigma$ chamada de volatilidade que diz o quão grande será as variações. Ou seja, ao invés de só $dt$, seria $\sigma dt$. Quanto maior for o valor da volatilidade, mais o mercado vai variar os preços.

O fato de $\sigma$ ser uma constante será discutido depois. Ou seja, até agora temos:

$$ dS = \sigma S dW $$

Além disso, teremos um termo que não é aleatório, chamado de drift. Ele vai basicamente adicionar a tendência exponencial que se nota nos mercados. Assim como o termo aleatório, este também será proporcional a $S$ e a uma constante \mu que dita o quão rápido será essa exponencial (chamado de drift rate):

$$ dS = \mu S dt $$

(Note que isso é $\frac{dS}{dt} = \mu S$ que tem como resultado da EDO a função exponencial).

Combinando os dois termos, temos o modelo de movimento browniano geométrico, usado para formular a equação de Black-Scholes:

$$ dS = \mu S dt + \sigma S dW $$

Podemos criar um rápido script de python para gerar uma lista de valores de $S$ em cada instante de tempo:

import numpy as np
np.random.seed(69420)

T = 10 # intervalo de tempo
dt = 0.01

# volatilidade e drift rate
sigma = 1.5
mu = 0.1

S = 1 # valor inicial
t = 0 # tempo inicial

while t < T:
    print(t, S)
    dW = np.random.normal(0, dt)
    dS = mu*S*dt + sigma*S*dW
    
    S += dS
    t += dt

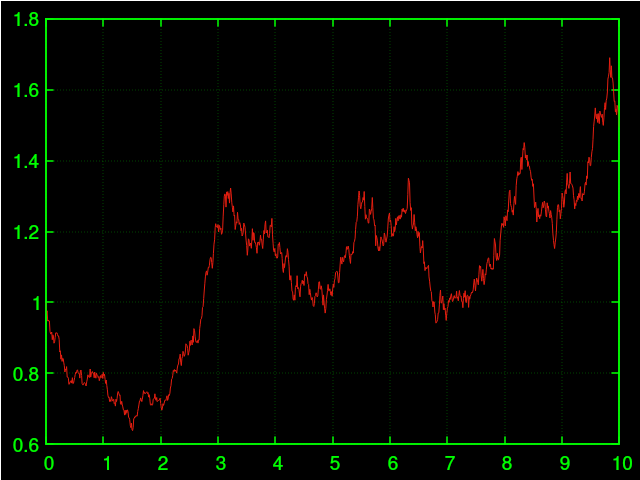Simulação Tendeu a crescer por conta de $\mu$ positivo, variou bastante por ter um $\sigma$ relativamente alto.

É ou não é igualzinho aos gráficos do mercado?? Não é. A seguir veremos os problemas.

O mercado não é tão simples assim

Modelar os preços apenas com um simples modelos estocástico assim não funciona. O motivo? Dados do futuro independem dos dados do passado. Basta ver que no código, o valor de $dS$ não depende de nenhum valor anterior, apenas o seu valor atual. De fato, se assumirmos esse modelo, é impossível lucrar em cima do mercado financeiro.

Apesar em situações “calmas” do mercado isso ser verdade, nós podemos notar certos padrões que seriam impossíveis com o nosso modelo atual.

Um deles se chama “volatility clustering”. No modelo que temos até agora, as variações são totalmente aleatórias, e $\sigma$ é constante. A realidade porém é que a volatilidade do mercado costuma se agrupar. Basta ver o índice de volatilidade VIX:

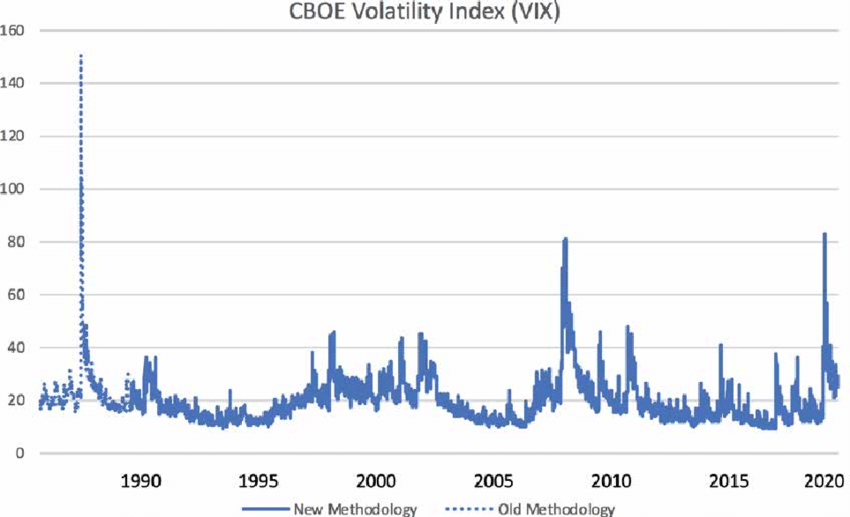VIX Note os picos em 2008 e 2020.

Para lidar com essa difícil verdade, existem vários modelos desenvolvidos “melhores”. Cada um reflete uma necessidade, nenhum vai conseguir replicar 100% corretamente a realidade da sociedade (porque, como falei, é complexo).

GARCH(p,q)

O primeiro modelo é o GARCH(p,q) (Generalized Autoregressive Conditional Heteroskedasticity).

Primeiro, algumas diferenças para como os econometristas lidam com os dados: ao invés de lidar com uma diferença de preços $dS$: $$ dS = S(t + dt) - S(t) $$ Nós iremos lidar com o log retorno: $$ r(t) = \ln(S(t + dt)) - \ln(S(t)) $$ Note que $e^{r(t)} = \frac{S(t + dt)}{S(t)}$, o que implica em $S(t+dt) = e^{r(t)}S(t)$.

Para simplificar a notação (e padronizar), ao invés de $S(t)$ eu vou escrever $S_t$, e ao invés de $S(t+dt)$ eu vou escrever $S_{t+1}$, e por aí vaí, cada instante é uma unidade do tempo. Similarmente, o log retorno vira $r_t$ e a volatilidade vira $\sigma_t$:

$$ r_t = \ln(S_{t+1}) - \ln(S_t)$$ $$ S_{t+1} = e^{r_t}S_t$$

Neste modelo, o a volatilidade é uma combinação linear dos quadrados tanto dos $q$ retornos anteriores como das $p$ volatilidades anteriores:

$$\sigma_t = \alpha_0 + \sum_{n=1}^q \alpha_n r_{t-n}^2 + \sum_{n=1}^p \beta_n \sigma_{t-n}^2$$

Então o retorno $r_t$ será dado por:

$$ r_t = \sigma_t \epsilon_t $$

Onde $\epsilon$ é normalmente distribuído, com desvio padrão $1$ e média $0$.

Supondo que $p = q = 1$ (ou seja, a volatilidade só depende dos valores intanteneamente anteriores), podemos escrever um código em python:

import numpy as np
np.random.seed(3)

alpha_0 = 0.0001
alpha_1 = 0.1
beta_1 = 0.8

N = 1000 # Número de instantes (Tf - Ti)/dt

#inicializar r, sigma, S
r = np.zeros(N)
sigma = np.zeros(N)
S = np.zeros(N)
S[0] = 1 # preço inicial

for t in range(1, N):
    sigma[t] = np.sqrt(alpha_0 + alpha_1*r[t-1]**2 + beta_1*sigma[t-1]**2)
    r[t] = sigma[t] * np.random.normal(0, 1)
    S[t] = S[t-1] * np.exp(r[t])

for t in range(0, N):
    print(t, S[t])

GARCH(1,1)

O mercado é fracamente eficiente

Muito legal os modelos que nós vimos, mas eles servem de quê? Nada que vai te gerar dinheiro. Como eu falei no post anterior, o mercado não eficiente a nível forte, mas parece ser bem eficiente a nível fraco. Inclusive, como demonstra um estudo que eu citei (doi:10.15388/Ekon.2014.2.3549), quanto maior e mais “maduro” um mercado, mais eficiente ele é.

Se você não quer ler muito, o resumo é que a eficiência fraca de um mercado, se refere a sua capacidade de lucrar com o histórico de valor delas.

Os modelos que eu mostrei até agora, se pautam apenas em valores crus. Nós estamos ignorando completamente que esses preços são resultado de decisões humanas. O histórico de preços pode até ser uma influência, mas existem vários outros fatores fundamentais.

Os melhores modelos não incorporam somente informação de preço, mas de todo tipo de coisa no mundo. E pode ter certeza que quem realmente tem dinheiro para influenciar o mercado já tem todo um time de quants que já tem todos esses algoritmos prontos rodando a todo vapor.

No próximo post, falarei sobre cassinos.