Computando geodésicas com python
Este post é uma continuação do anterior.
Geodésicas
A equação geral é dada por:
$$ \frac{\partial^2 \gamma^\mu}{\partial t^2} - \sum_{\alpha, \beta} \Gamma^\mu_{\alpha \beta} \frac{\partial \gamma^\alpha}{\partial t}\frac{\partial \gamma^\beta}{\partial t} = 0$$
Onde $\gamma: I \to M$ é a curva geodésica na variedade $M$, e cada índice se refere a uma coordenada da variedade (i.e, $\gamma(t) = (\gamma^0(t), \gamma^1(t), \ldots)$). $\Gamma^\mu_{\alpha \beta}$ são os símbolos de christoffel daquela variedade, especificando sua curvatura.
Por exemplo, se nossa variedade é um torus de raio $R$ e tubo de raio $a$, então a equação é dada por um sistema de duas variáveis:
$$ \frac{\partial^2 \theta}{\partial t^2} = 2 \frac{a\sin(\phi)}{R + a\cos(\phi)} \frac{\partial \theta}{\partial t}\frac{\partial \phi}{\partial t}$$
$$ \frac{\partial^2 \phi}{\partial t^2} = \left(\frac{R}{a}\sin(\phi) + a\cos(\phi)\right) \left(\frac{\partial \theta}{\partial t}\right)^2$$
Que pode ser transformada em um sistema de quatro variáveis no formato $\vec{y}' = f(t, \vec{y})$:
$$ \frac{d}{dt} \begin{bmatrix} \theta \\ \phi \\ \dot{\theta} \\ \dot{\phi} \end{bmatrix} = \begin{bmatrix} \dot{\theta} \\ \dot{\phi} \\ \frac{2a\sin(\phi)}{R + a\cos(\phi)} \dot{\theta}\dot{\phi} \\ \left(\frac{R}{a}\sin(\phi) + a\cos(\phi)\right) \dot{\theta}^2 \end{bmatrix} $$
Que pode ser implementado como visto no post anterior:
import numpy as np
from scipy.integrate import solve_ivp
R = 3
a = 1
def f(t, y):
theta, phi, dtheta, dphi = y
return [
dtheta,
dphi,
2*( (a*np.sin(phi)) / (R + a*np.cos(phi))) * dtheta * dphi,
((R*np.sin(phi))/a + a*np.cos(phi)) * dtheta**2
]
t_span = [0, 1]
t_eval = np.linspace(0, 1, 1000)
pos_i = [0, 0] #posição inicial
vel_i = [4, -1] #velocidade inicial
y0 = [pos_i[0], pos_i[1], vel_i[0], vel_i[1]]
sol = solve_ivp(f, t_span, y0, t_eval=t_eval)
E dessa solução sol podemos passar para uma função que faça a imersão do torus no espaço $\mathbb{R}^3$:
def r(theta, phi):
return (
(R + a*np.cos(phi))*np.cos(theta),
(R + a*np.cos(phi))*np.sin(theta),
a*np.sin(phi)
)
for i in range(len(sol.t)):
theta = sol.y[0][i]
phi = sol.y[1][i]
x, y, z = r(theta, phi)
print(x, y, z)
Esses dados podem ser colocados no gnuplot para obtermos uma visualização:
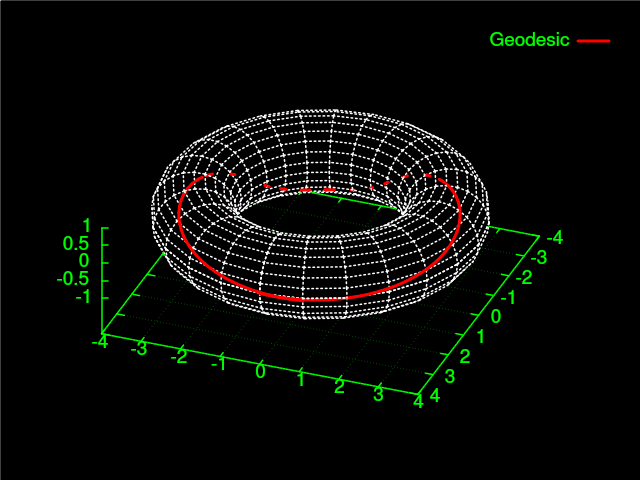
Mas esse negócio de “velocidade inicial” é um saco. Seria muito mais interessante nós termos uma posição final $x_f$, ao invés de uma velocidade inicial que é um mistério total de onde vai parar.
Aqui, usamos o método de tiro. Em termos gerais funciona assim:
Escrevemos uma função $F(v)$ que recebe uma velocidade inicial $v$ e calcula uma posição final obtida $x_v$. Então, a função retorna a norma da diferença entre a posição final obtida e a posição final desejada: $F(v) = ||x_v - x_f||$.
Isso significa que $F$ retorna o quão errada está nossa velocidade inicial para uma velocidade final desejada. Queremos, portanto minimizar o erro $F$, ou numa situação ideal, termos $F = 0$.
Felizmente, o scipy tem uma função que faz essa minimização: o minimize do scipy.optimize.
from scipy.optimize import minimize
pos_f = [np.pi/2, np.pi/2]
def F(v):
y0 = [pos_i[0], pos_i[1], v[0], v[1]]
sol = solve_ivp(f, [0, 1], y0, t_eval=np.linspace(0,1,50))
shoot_pos = [sol.y[0][-1], sol.y[1][-1]]
error = np.subtract(shoot_pos, pos_f)
error_norm = np.sqrt(error[0]**2 + error[1]**2)
return error_norm
vel_i = minimize(F, [0,0]).x
O código inteiro ficará no final da página. Plotando com o gnuplot, temos a seguinte imagem:
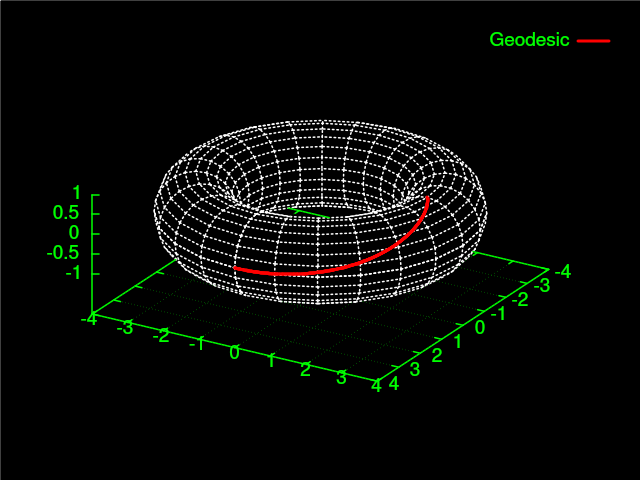
É visível que foi feito um quarto de volta tanto no anel maior quando no tubo. Isso reflete o fato que nossa posição final era $(\frac{\pi}{2}, \frac{\pi}{2})$.
As técnicas usadas podem ser usadas em métricas mais complexas. Pretendo fazer algum post sobre buracos de minhoca em breve.
Código:
import numpy as np
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
R = 3
a = 1
def f(t, y):
theta, phi, dtheta, dphi = y
return [
dtheta,
dphi,
2*( (a*np.sin(phi)) / (R + a*np.cos(phi))) * dtheta * dphi,
((R*np.sin(phi))/a + a*np.cos(phi)) * dtheta**2
]
t_span = [0, 1]
t_eval = np.linspace(0, 1, 1000)
pos_i = [0, 0]
pos_f = [np.pi/2, np.pi/2]
def F(v):
y0 = [pos_i[0], pos_i[1], v[0], v[1]]
sol = solve_ivp(f, [0, 1], y0, t_eval=np.linspace(0,1,50))
shoot_pos = [sol.y[0][-1], sol.y[1][-1]]
error = np.subtract(shoot_pos, pos_f)
error_norm = np.sqrt(error[0]**2 + error[1]**2)
return error_norm
vel_i = minimize(F, [0,0]).x
y0 = [pos_i[0], pos_i[1], vel_i[0], vel_i[1]]
sol = solve_ivp(f, t_span, y0, t_eval=t_eval)
def r(theta, phi):
return (
(R + a*np.cos(phi))*np.cos(theta),
(R + a*np.cos(phi))*np.sin(theta),
a*np.sin(phi)
)
for i in range(len(sol.t)):
theta = sol.y[0][i]
phi = sol.y[1][i]
x, y, z = r(theta, phi)
print(x, y, z)